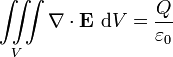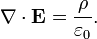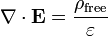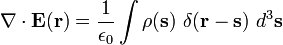تبلیغات

چند ضلعی ها

چند ضلعيها

تعريف چند ضلعي :
هر خط شكسته بسته را چند ضلعي مي نامند . مثلث يك چند ضلعي (سه ضلعي) است. اگر يكي از زواياي داخلي چند ضلعي بزرگتراز 180 درجه باشد،چند ضلعي را مقعر و در غير اين صورت چند ضلعي را محدب مي نامند.

نكته 1 :
مجموع اندازه هاي زواياي هر n ضلعي برابر با درجه است.
براي مثال ، مجموع اندازه هاي زواياي يك هفت ضلعي برابر با درجه است.

نكته 2 :
تعداد قطرهاي هر n ضلعي محدب برابر با

½ (n)(n-3)

است.

نكته 3 :
در چند ضلعيهاي منتظم با تعداداضلاع زوج، اضلاع مقابل بر هم ، با هم موازيند.

نكته 4 :
در هر چند ضلعي منتظم با تعداد اضلاع فرد، عمودمنصف هر ضلع ، نيمساز زاويه مقابل به آن ضلع است. كه اين عمود منصف (يا نيمساز) محور تقارن آن چند ضلعي است.

متوازي الاضلاع

چهار ضلعي است كه هر دو ضلع آن موازي باشند. در متوازي الاضلاع، فاصله هر دو ضلع مقابل به هم را ارتفاع مي نامند.

ويژگيهاي متوازي الاضلاع

الف) در هر متوازي الاضلاع، اضلاع مقابل با هم برابر هستند.
ب)درهر متوازي الاضلاع زاويه هاي مقابل برابرند و هر دو زاويه مجاور يك ضلع مكمل يكديگرند. همچنين مجموع دو زاويه مجاور برابر 180 درجه است.
ج) در هر متوازي الاضلاع قطرها منصف يكديگرند.
د) در هر متوازي الاضلاع نقطه تقاطع دو قطر مركز تقارن آن شكل است.
ه‍) مساحت متوازي الاضلاع برابر با حاصلضرب قاعده در ارتفاع وارد بر آن است.

ز) در هر متوازي الاضلاع، نيمسازهاي داخلي دو به دو بر هم عمودند.

لوزي

لوزي متوازي الاضلاعي است كه چهار ضلع آن با هم برابر باشند. بنابراين لوزي كليه ويژگيهاي متوازي الاضلاع را دارد.
مساحت و محيط لوزي :
مساحت لوزي برابر نصف حاصلضرب اندازه هاي دو قطر است.

نكته 1 :
از هر لوزي يك دايره محاطي مي گذرد.

كايت

كايت يا شبه لوزي ، چهار ضلعي محدبي است كه داراي دو جفت اضلاع مجاور مساوي با دو اندازه مختلف باشد. در واقع كايت چهار ضلعي محدبي است كه داراي دو قطر عمود بر هم باشد و فقط يكي از قطرها منصف قطر ديگر باشد. قطري كه منصف قطر ديگر است، محور تقارن كايت و همچنين نيمساز دو زاويه مقابل است. مساحت كايت مانند مساحت لوزي محاسبه مي شود.

مستطيل

مستطيل متوازي الاضلاعي است كه يك زاويه آن قائمه باشد. بنابراين مستطيل كليه ويژگيهاي متوازي الاضلاع را داراست. خطي كه وسط دو ضلع مقابل را به هم وصل كند محور تقارن مستطيل است. بنابراين مستطيل دو محور تقارن دارد.
نكته 1 :
مساحت مستطيل برابر حاصلضرب طول در عرض آن است.
نكته 2 :
بر مستطيل يك دايره محيطي مي گذرد.

مربع

مربع مستطيلي است كه چهار ضلع آن با هم مساوي باشد و يا مي توان گفت ، مربع لوزي است كه يك زاويه آن قائمه باشد. بنابراين مربع كليه ويژگيهاي متوازي الاضلاع، مستطيل و لوزي را دارد.

نكته 1 :
در هر مربع قطرها بر هم عمود و با هم برابر و هر كدام محور تقارن شكل هستند.
نكته 2 :
مربع چهار محور تقارن (به تعداد اضلاع) دارد. مربع يك چهار ضلعي منتظم است و كليد ويژگيهاي چند ضلعي منتظم را داراست.
مساحت و محيط مربع : مساحت مربع برابر مجذوب يك ضلع است.

ذوزنقه

هر چهار ضلعي كه فقط دو ضلع آن با هم موازي باشند، ذوزنقه ناميده مي شود. دو ضلع موازي را قاعده ها، و دو ضلع غيرموازي را ساقها مي نامند. اگر دو ساق ذوزنقه با هم مساوي باشند ذوزنقه را متساوي الساقين مي نامند، اگر يكي از ساقها بر دو قاعده عمود باشد ذوزنقه را قائم الزاويه مي نامند.

نكته 1 :
در هر ذوزنقه دو زاويه مجاوز بر هر ساق مكمل يكديگرند.
نكته 2 :
در هر ذوزنقه متساوي الساقين دو قطر با هم و همچنين دو زاويه مجاور به هر قاعده با هم برابر هستند.
نكته 3 :
پاره خطي كه دو سر آن وسط هاي دو ساق ذوزنقه باشد، موازي دو قاعده آن ذوزنقه و اندازه آن برابر نصف مجموع اندازه هاي دو قاعده ذوزنقه است.

مساحت ذوزنقه :
مساحت ذوزنقه با نصف حاصلضرب مجموع دو قاعده درارتفاع آن برابر است.
چهار ضلعي هاي محيطي
چهار ضلعي محيطي چهار ضلعي است كه اضلاع آن بر يك دايره مماس باشند.

نكته 1 :
درهر چهار ضلعي محيطي مجموع دو ضلع مقابل با مجموع دو ضلع مقابل ديگر برابر است.
چهارضلعي هاي محاطي
چهار ضلعي محاطي چهار ضلعي است كه رأسهاي آن بر يك دايره واقع باشد.

نكته 1 :
در هر چهار ضلعي محاطي مجموع دو زاويه مقابل 180 درجه است.

ارسال شده در : چهار شنبه 30 مهر 1393 ساعت: 15:51 + تعداد بازديد : 438

نویسنده : حسین نوروزی

دسته بندی ها : ریاضی , ,

» نظرات()
می پسندم 0 نمی پسندم 0

اعداد اول

عدد اول

از ویکی‌پدیا، دانشنامهٔ آزاد

غربال اراتوستنس الگوریتمی ساده و قدیمی برای یافتن همهٔ اعداد اول تا عدد صحیح برگزیده است. این الگوریتم پیش از غربال آتکین، که سریع‌تر و پیچیده‌تر بود، مورد استفاده قرار می‌گرفت. غربال اراتوستنس رااراتوستنس، ریاضیدان یونان باستان در قرن سوم پیش از میلاد ابداع کرد.

عدد اول عددی طبیعی بزرگ‌تر از ۱ است که بر هیچ عدد مثبتی بجز خود و ۱بخش‌پذیر نباشد. تنها استثنا عدد ۱ است که جزو این اعداد قرار نمی‌گیرد. اگرعددی طبیعی وبزرگ‌تر از ۱ اول نباشد مرکب است.

رقم یکان اعداد اول بزرگ‌تر از ۱۰ فقط ممکن است ارقام ۱، ۳، ۷، و ۹ باشد.

پیدا کردن رابطه‌ای جبری برای اعداد اول جزو یکی از معماهای ریاضی باقیمانده است و هنوز کسی به فرمولی برای آنها دست نیافته است.

دنبالهٔ اعداد اول به این صورت شروع می‌شود:

۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹، ۲۳، ۲۹، ۳۱، ۳۷، ۴۱، ۴۳، ۴۷، ۵۳، ۵۹، ۶۱، ۶۷،۷۱، ۷۳، ۷۹، ۸۳، ۸۹، ۹۷، ۱۰۱، ۱۰۳، ۱۰۷، ۱۰۹، ۱۱۳، ۱۲۷، ۱۳۱، ۱۳۷، ۱۳۹^[۱]

محتویات

[نهفتن]

قضیه‌ها[ویرایش]

قضیه ۱: تعداد اعداد اول بی‌نهایت است.

به این اثبات دقت کنیداز برهان خلف استفاده می کنیم:

فرض خلف : اعداد اول متناهی است.

اعداد اول را در هم ضرب می کنیم.

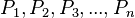
$P_1,P_2,P_3, ... ,P_n$

ضرب اعداد از $P_i$ بزرگ‌تراست.

$P_1 \times P_2 \times P_3 \times ... \times P_n> P_i$

$P_1 \times P_2 \times P_3 \times ... \times P_n + 1> P_i$

$P_1 \times P_2 \times P_3 \times ... \times P_n + 1 = P_{i_1} ... P_{i_k}$

$P_1 \times P_2 \times P_3 \times ... \times P_n + 1 = P_i \times X$

$P_{i_1} \times ... \times P_{i_k} = P_i \times X$

$P_1 \times P_2 \times P_3 \times ... \times P_n +1 = Y+1$

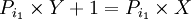
$P_{i_1} \times Y + 1 = P_{i_1} \times X$

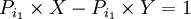
$P_{i_1} \times X - P_{i_1} \times Y = 1$

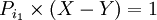
$P_{i_1}\times(X-Y) = 1$

$P_{i_1} = 1$

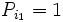
که عدد ۱ جزو اعداد اول نیست پس به تناقض می رسیم و فرض خلف باطل است. اعداد اول نامتناهی هستند.

قضیه 2 (قضیه اساسی حساب): هر عدد طبیعی بزرگ‌تر از ۱ را می‌توان به شکل حاصل‌ضرب اعدادی اول نوشت.
قضیه 3 (قضیه چبیشف):اگر n عددی طبیعی و بزرگ‌تر از ۳ باشد، حتما" بین n و ۲n عدد اولی وجود دارد.
قضیه 4 (قضیه اردیش (تعمیم قضیه چبیشف)): برای هر عدد طبیعی k، وجود دارد یک عدد طبیعی مثل N، که برای هر n>N ،بین n و 2n،

k عدد اول وجود دارد.

قضایای اعداد اول[ویرایش]

قضیه گلدباخ (تاکنون اثبات نشده): هر عدد زوج را می‌توان به شکل جمع دو عدد اول نوشت.

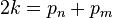
$2k=p_n+p_m$

مثال:

$4= 2+ 2$

$6= 3+ 3$

$8= 5+ 3$

$10= 5+ 5$

$12= 7+ 5$

$14= 7+ 7$

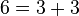
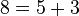
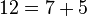
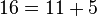
$16=11+ 5$

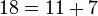
$18=11+ 7$

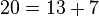
$20=13+ 7$

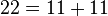
$22=11+11$

$24=13+11$

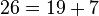
$26=19+ 7$

تابع شمارش اعداد اول[ویرایش]

در ریاضیات تابع شمارش اعداد اول تابعی است که برای بیان تعداد اعداد اول به کار می‌رود و آن را با نماد \pi(x) نمایش می‌دهند.

ریاضیدان فرانسوی پیر دوسارارت ثابت کرد که برای x ≥ ۵۹۹ رابطه زیر برقرار است:

$\frac{x}{\ln x}\left(1+\frac{1}{\ln x}\right) < \pi(x) < \frac{x}{\ln x}\left(1+\frac{1}{\ln x}+\frac{2.51}{(\ln x)^2}\right).$

همچنین ثابت کرد که برای هر x ≥ ۳۵۵۹۹۱:

$\frac {x}{\ln x + 2} < \pi(x) < \frac {x}{\ln x - 4}$

بعدها ثابت شد که برای هر ε>۰ وجود دارد عددی طبیعی ماننده s که برای هر x>s رابطه زیر برقرار است:

$\frac {x}{\ln x - (1-\varepsilon)} < \pi(x) < \frac {x}{\ln x - (1+\varepsilon)}.$

قضیه اعداد اول (prime number theorem)[ویرایش]

اگر $\pi(x)$ تعداد اعداد اول کمتر از $x$ باشد

آنگاه $\lim_{x \to \infty} \frac{\pi(x)}{x/ln(x)} = 1$

$x$	$\pi(x)$	$\frac{\pi(x)}{x/ln(x)}$
10	4	0.921
10²	25	1.151
10³	168	1.161
10⁴	1,229	1.132
10⁵	9,592	1.104
10⁶	78,498	1.084
10⁷	664,579	1.071
10⁸	5,761,455	1.061
10⁹	50,847,534	1.054
10¹⁰	455,052,511	1.048
OEIS	A006880	A057835

با استفاده از قضیه اعداد اول می توان اثبات کرد که:

$\lim_{x \to \infty} \frac{p(x)}{x \ln(x)} = 1$

که در آن تابع 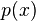$p(x)$ ، تابع مولد اعداد اول باشد. یعنی x امین عدد اول $p(x)=$

اثبات مطلب بالا به شرح زیر است:

می دانیم $\lim_{x \to \infty} \frac{\pi(x)}{x/ln(x)} = 1$

$\pi(x)\sim\frac{x}{\ln x}.\!$

می دانیم توابع 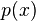$p(x)$ و $\pi(x)$ معکوس هم هستند. یعنی:

$p^{-1}\left( \, x \, \right) = \pi(x)$

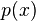در نتیجه می توان با حل معادله $\pi(x)=x$ تابع $p(x)$ را یافت.

می دانیم $\pi(x)\sim\frac{x}{\ln x}.\!$

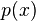پس با حل معادله $\frac{x}{\ln x}=x$ می توان هم ارزی برای $p(x)$ یاقت.

به روش تکرار ساده معادله را حل میکنیم.

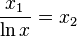
$\frac{x_1}{\ln x}=x_2$

${x_1}=x_2 \ln(x)$

$p(x)=x \ln(x)$

اما باید توجه داشت چون به جای $\pi(x)$ از تابع هم ارز آن استفاده شده پس:

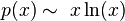
$p(x)\sim\ x \ln(x)$

در نتیجه:

$\lim_{x \to \infty} \frac{p(x)}{x \ln(x)} = 1$

قضیه ویلسون راهی برای تشخیص اعداد اول[ویرایش]

قضیه ویلسون راهی برای تشخیص اعداد اول است. این قضیه بیان می‌کند به ازای هر عدد اول مانند $\; p$ داریم $\;(p-1)! \equiv -1 \pmod{p}$

این قضیه دوشرطی است بنابراین راهی برای تشخیص اعداد اول از مرکب است یعنی:

برای هر عدد صحیح x اگر رابطه زیر برقرار باشد آنگاه x عددی اول است در غیر این صورت x عددی غیر مرکب است.

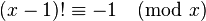
$\;$ $\;(x-1)! \equiv -1 \pmod{x}$

این قضیه تعمیم هایی به شکل زیر دارد:

تعمیم گاوس: کارل فریدریش گاوس ریاضیدان آلمانی در سال ۱۸۰۰ میلادی ثابت کرده که برای هر عدد طبیعی m>۲ عدد اول p

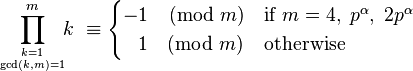
$\prod_{k = 1 \atop \gcd(k,m)=1}^{m} \!\!k \ \equiv \begin{cases} -1 \pmod{m} & \text{if } m=4,\;p^\alpha,\;2p^\alpha \\ \;\;\,1 \pmod{m} & \text{otherwise} \end{cases}$

در اینجا $\alpha$ عددی صحیح و مثبت است.

کشف و محاسبه[ویرایش]

بزرگ‌ترین عدد اول کشف شده برابر دو به توان 57میلیون و 885هزار و 161منهای یک است.این عدد یک عدد مرسن است. عدد مرسن عددی است که برابر ۲ به توان n منهای یک است. گروه محاسباتی سراوان دیتا که یک گروه محاسباتی ارانی می‌باشد که در زمینه‌های مختلف محاسباتی از جمله اعداد اول فعالیت می‌کند اعداد بسیاری را کشف و محاسبه کرده از جمله تمام اعداد اول یک تا دویست میلیون

جایزه‌ها برای پیدا کردن اعداد اول[ویرایش]

موسسه Electronic Frontier Foundation جایزه‌ای به مبلغ صدهزار دلار برای اولین کسی که یک عدد اول با حداقل 10 میلیون رقم پیدا کند در نظر گرفته است.همچنین مبلغ 150 هزار دلار برای کسی که یک عدد اول با 100 میلیون رقم و 250 هزار دلار برای 1 میلیارد رقم در نظر گرفته شده است.این موسسه ممکن است مبلغ 100 هزار دلار برای دپارتمان ریاضی دانشگاه UCLA که موفق به کشف یک عدد اول 13 میلیون رقمی شدند پرداخت کند.

الگوهای توزیع اعداد اول[ویرایش]

یکی از مسائل مورد توجه ریاضی‌دانان، چگونگی توزیع و ترتیب قرارگرفتن اعداد اول درون رشته اعداد طبیعی است. این چگونگی دارای الگوهایی است که یکی از آنها به «الگوی پیشرفت عددی» معروف است.
مثلاً اگر به عدد ۵ که عددی اول است، ۶ واحد اضافه کنیم به ۱۱ و اگر به ۱۱، ۶ واحد اضافه کنیم به ۱۷ و اگر دوباره اضافه کنیم، به ۲۳ و ۲۹ می‌رسیم که همگی اعدادی اولند. اما با اضافه کردن ۶ واحد دیگر به ۳۵ می‌رسیم که عددی اول نیست و الگو متوقف می‌گردد.

مسئله مورد توجه اینست که در هر الگوی پیشرفت چند عدد اول پیش از رسیدن به اولین عدد غیر اول، بدست می‌آیند؟ طولانی‌ترین رشته‌ای که تاکنون بدست آمده، ۲۲ عدد اول را شامل است. اولین عدد اول این رشته ۱۱۴۱۰۳۳۷۸۵۰۵۵۳ بوده که اگر عدد ۴۶۰۹۰۹۸۶۹۴۲۰۰ به آن اضافه شود عدد اول بعدی بوجود می‌آید و می‌توان ۲۲ بار عدد مذکور را به اعداد اول مرحله قبل افزود و عدد اولی جدید بدست آورد. دو ریاضی‌دان اثبات کرده‌اند برای هر رشته از اعداد اول می‌توان به یک رشته عددی رسید.

ارسال شده در : پنج شنبه 24 مهر 1393 ساعت: 9:45 + تعداد بازديد : 1215

نویسنده : حسین نوروزی

دسته بندی ها : ریاضی , ,

» نظرات()
می پسندم 0 نمی پسندم 0

قانون گاوس

از ویکی‌پدیا، دانشنامهٔ آزاد

قانون گاوس در فیزیک با نام قضیه شار گاوس هم شناخته شده که قانونی است در ارتباط با توزیع بار الکتریکی که پیامد آن میدان الکتریکی است قانون گاوس توضیح می‌دهد که:

شار الکتریکی کل در هر سطح بسته‌ای برابر است با بار کل احاطه شده توسط آن سطح

این قانون توسط کارل فردریک گاوس در سال ۱۸۳۵ فرمولبندی شد ولی در سال ۱۸۶۷ منتشر گشت. این قانون یکی از چهار معادله ماکسول است که اساس الکترودینامیک کلاسیک را تشکیل می‌دهند، سه تای دیگر عبارت اند از:قانون گاوس برای مغناطیس، قانون القاء فارادی، و قانون آمپر به تصحیح ماکسول. از قانون گاوس می‌توان برای استخراج قانون کولن استفاده کرد و بالعکس. با اعمال مناسب قضیه واگرایی به قانون کولن , قانون گاوس نتیجه می‌شود.
قانون گاوس معمولاً به فرم انتگرالی زیر بیان می‌شود:

\oint_S \mathbf{E} \cdot \mathrm{d}\mathbf{A} = \frac{Q}{\varepsilon_0},

که در آن سمت چپ تساوی انتگرال سطحی است که نشر شار الکتریکی را از سطح بسته S بیان می‌کند، و سمت راست تساوی بار کل محصور شده در همان سطح S تقسیم بر ثابت الکتریکی است.

قانون گاوس همچنین فرم دیفرانسیلی به شکل زیر دارد:

\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}

که در آن E · ∇ دیورژانس میدان الکتریکی است و ρ چگالی بار است. فرم انتگرالی و دیفرانسیلی با قضیه دیورژانس به هم مرتبط می‌شوند. هر یک از این اشکال دیفرانسیلی و انتگرالی را می‌توان به دو فرم دیگر بیان کرد: از دید ارتباط بین میدان الکتریکی E و بار الکتریکی کل، یا از دید جابجایی میدان الکتریکی D و بار الکتریکی آزاد. قانون گاوس تشابه ریاضیاتی زیادی با تعدادی از قوانین فیزیک در سایر زمینه‌ها دارد، مثل قانون گاوس در مغناطیس و قانون گاوس در جاذبه. در واقع، هر «قانون مربع معکوس» را می‌توان به شکل مشابهی با قانون گاوس فرمولبندی کرد: برای مثال، خود قانون گاوس خود اساساً برابر با مربع معکوس قانون کولن است، و قانون گاوس برای جاذبه اساساً با مربع معکوس قانون جاذبه نیوتون برابر است.

محتویات

[نهفتن]

از دیدگاه بار کل[ویرایش]

فرم انتگرالی[ویرایش]

برای حجم V با سطح S، قانون گاوس بیان می‌کند که

\Phi_{E,S} = \frac{Q}{\varepsilon_0}

که Φ_E,S شار الکتریکی در S است، Q بار کل در حجم V است، و ε_۰ ثابت الکتریکی است. شار الکتریکی از انتگرال گیری روی سطح Sبدست می‌آید:

\oint_S \mathbf{E} \cdot \mathrm{d}\mathbf{A}

که E میدان الکتریکی است و dA نشانگر برداری از المان بی نهایت کوچک سطح می‌باشد و (.) به عنوان ضرب داخلی برداری به کار می‌رود.

به کارگیری فرم انتگرالی[ویرایش]

اگر میدان الکتریکی همه جا معلوم باشد، قانون گاوس کار را خیلی راحتتر می‌کند، در اصل، برای یافتن توزیع بار الکتریکی: باری را که در هر ناحیه داده شده می‌تواند با یکپارچگی میدان الکتریکی و یافتن شار استنباط کرد. با این حال، بیشتر اوقات، این مشکل معکوسی است که باید حل شود: یعنی توزیع بار الکتریکی معلوم است، و میدان الکتریکی باید محاسبه شود. این خیلی مشکل تر است، زمانی که شما شار کل عبوری از سطح را می‌دانید، که این تقریباً هیچ اطلاعاتی در مورد میدان الکتریکی نمی‌دهد، که خود می‌تواند از روی الگوی پیچیده‌ای خودسرانه وارد و خارج سطح شود.

فرم دیفرانسیلی[ویرایش]

شکل دیفرانسیلی، قانون گاوس بیان می‌دارد که:

\mathbf{\nabla} \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}

که · ∇نشان دهنده واگرایی یا همان دیورژانس، E میدان الکتریکی، و ρ چگالی بار کل است، و ε_۰ ثابت الکتریکی است. این معادله از لحاظ ریاضی بنا به قضیه دیورژانس با فرم انتگرالی معادل است.

هم ارزی فرم دیفرانسیلی و انتگرالی[ویرایش]

فرم‌های دیفرانسیلی و انتگرالی از دیدگاه ریاضی معادل اند، از طریق قضیه دیورژانس. به بیان دقیق تر: فرم انتگرالی قانون گاوس به این صورت است که:

\oint_S \mathbf{E} \cdot \mathrm{d}\mathbf{A} = \frac{Q}{\varepsilon_0}

برای هر سطح بسته S که بار Q را در بر می‌گیرد. با قضیه دیورژانس، این معادله برابر است با:

\iiint\limits_V \nabla \cdot \mathbf{E} \ \mathrm{d}V = \frac{Q}{\varepsilon_0}

برای هر حجم V که بار Q را در بر می‌گیرد. با توجه به ارتباط بین بار الکتریکی و چگالی بار، این تساوی معادل است با:

\iiint\limits_V \nabla \cdot \mathbf{E} \ \mathrm{d}V = \iiint\limits_V \frac{\rho}{\varepsilon_0} \ \mathrm{d}V

برای هر حجم V. برای این که این معادله به طور همزمان برای هر حجم ممکن V برقرار باشد، این شرط لازم و کافی است که معادلات زیر انتگرال برابر باشند. بنابراین، این تساوی معادل است با

\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}.

پس معادلات دیفرانسیل و انتگرال معادل هستند.

از دیدگاه بار آزاد[ویرایش]

بار آزاد در مقابل بار مقید[ویرایش]

بار الکتریکی که در ساده‌ترین موقعیت‌های کتاب درسی بیان می‌شود در میان بار الکتریکی آزاد طبقه بندی می‌شود، برای مثال، باری که در الکترواستاتیک جابجا می‌شود، یا باری که روی صفحه‌های خازن ذخیره می‌شوند. در عوض بار مقید فقط در مورد چارچوب دی الکتریکبیان می‌شود و موادی که قابلیت قطبی شدن دارند.(تمام مواد تا حدی قابلیت قطبش دارند.) زمانی که موادی این چنین در یک میدان الکتریکی خارجی قرار می‌گیرند، الکترون‌ها در قید اتم‌های خود می‌مانند، اما در پاسخ به میدان الکتریکی یک تغییر فاصله میکروسکوپی با اتم خود می‌دهند، بنابر این الکترون‌های یک سمت بیشتر از سمت دیگر اتم می‌شود. همه این جابجایی‌های میکروسکوپیک جمع می‌شوند تا یک شبکه توزیع بار را تشکیل دهند، و این به منزله وجود بار مقید است. همه بارها از دیدگاه میکروسکوپیک اساساً یکسان هستند، اغلب دلایل عملی برای تمایز بین بار مقید و بار آزاد وجود دارد. یکی از دلایل اساس قانون گاوس است، که از لحاظE، در اکثر موارد در معادلات برای محاسبات و استفاده از D باید بار را به صورت بار آزاد در نظر بگیریم.

فرم انتگرالی[ویرایش]

این فرمولبندی از قانون گاوس بیان می‌دارد که، برای هر حجمV در فضا، با سطح S، رابطه زیر برقرار است:

\Phi_{D,S} = Q_{\mathrm{free}},\!

که Φ_D,S شار جابجایی میدان الکتریکی D از سطح S، و 'Q_free بار آزادی است که در حجم V قرار دارد. شار Φ_D,S مشابه شار میدان الکتریکی Φ_E,S که شار E از سطح S است تعریف شده. به ویژه که آن از انتگرال سطح بدست می‌آید

\Phi_{D,S} = \oint_S \mathbf{D} \cdot \mathrm{d}\mathbf{A}.

فرم دیفرانسیلی[ویرایش]

فرم دیفرانسیلی قانون گاوس، که فقط شامل بارهای آزاد می‌شود، بیان می‌دارد:

\mathbf{\nabla} \cdot \mathbf{D} = \rho_{\mathrm{free}}

که D · ∇ دیورژانس جابجایی میدان الکتریکی است، و ρ_free چگالی بار آزاد می‌باشد. فرم دیفرانسیلی و فرم انتگرالی از لحاظ ریاضیاتی معادل اند.

بیان هم ارزی بار کل و بار آزاد [ویرایش]

در مواد خطی[ویرایش]

در مواد همگن، ایزوتروپیک، ناپاشنده خطی یک ارتباط ساده و زیبا بین E و D هست:

\varepsilon \mathbf{E} = \mathbf{D}

که ε ضریب گذر دهی الکتریکی ماده‌است. تحت این شرایط هنوز یک جفت از فرمول‌های قانون گاوس باقی است:

\Phi_{E,S} = \frac{Q_{\mathrm{free}}}{\varepsilon}

\mathbf{\nabla} \cdot \mathbf{E} = \frac{\rho_{\mathrm{free}}}{\varepsilon}

ارتباط با قانون کولن[ویرایش]

استخراج قانون گاوس از قانون کولن[ویرایش]

قانون گاوس می‌تواند از قانون کولن استخراج شود، قانون کولن بیان می‌دارد که میدان الکتریکی حاصل از بار ثابت است:

\mathbf{E}(\mathbf{r}) = \frac{q}{4\pi \epsilon_0} \frac{\mathbf{e_r}}{r^2}

که:e_r بردار یکه شعاعی است، r شعاع است، :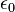 $\epsilon_0$ هم ثابت الکتریکی است، q بار ذره‌است، که فرض شده در مبدا قرار دارد.

با استفاده از این بیان قانون کولن، ما میدان کل را در فاصله r با استفاده از انتگرال گیری برای جمع تمام میدان‌ها در r از بارهای بی نهایت خورد در فضای s را داریم:

\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi\epsilon_0} \int \frac{\rho(\mathbf{s})(\mathbf{r}-\mathbf{s})}{|\mathbf{r}-\mathbf{s}|^3} d^3 \mathbf{s}

اگر ما از هر دو طرف تساوی دیورژانس بر حسب r بگیریم داریم

\nabla \cdot \left(\frac{\mathbf{s}}{|\mathbf{s}|^3}\right) = 4\pi \delta(\mathbf{s})

که (δ(s تابع دلتای دیراک است، حاصل به شکل زیر بدست می‌دهد:

\nabla\cdot\mathbf{E}(\mathbf{r}) = \frac{1}{\epsilon_0} \int \rho(\mathbf{s})\ \delta(\mathbf{r}-\mathbf{s})\ d^3 \mathbf{s}

با استفاده از خاصیت غربالگری تابع دلتای دیراک می‌رسیم به:

\nabla\cdot\mathbf{E}(\mathbf{r}) = \rho(\mathbf{r})/\epsilon_0

که همان فرم دیفرانسیلی قانون گاوس هست، درست همان طور که انتظار داشتیم.

استخراج قانون کولن از قانون گاوس[ویرایش]

به صرف گفتار، قانون کولن را نمی‌توان از قانون گاوس استخراج کرد چون قانون گاوس هیچ اطلاعاتی در مورد کرل یا تاو E نمی‌دهد. با این وجود، قانون کولن می‌تواند از قانون گاوس اثبات شود، بعلاوه، میدان الکتریکی حاصل از بار نقطه‌ای به شکل کروی متقارن است(این فرض مثل خود قانون کولن است، که وقتی بار ثابت است دقیقاً صحت دارد، و وقتی بار در حرکت باشد تقریباً درست است).

قرار دادن S در فرم انتگرالی قانون گاوس سطح کره‌ای به دست می‌دهد به شعاع r، که بار نقطه‌ای Q در مرکز قرار دارد:

\oint_{S}\mathbf{E}\cdot d\mathbf{A} = Q/\varepsilon_0

با فرض تقارن کروی، حاصل انتگرال مقدار ثابتی می‌شود که می‌توان از زیر انتگرال خارج کرد، و نتیجه می‌دهد:

4\pi r^2\hat{\mathbf{r}}\cdot\mathbf{E}(\mathbf{r}) = Q/\varepsilon_0

که $\hat{\mathbf{r}}$ بردار یکه شعاعی است که سمت بار نقطه‌ای را که در فاصله r هست نشان می‌دهد، دوباره با استفاده از تقارن کروی، E در راستای شعاعی را به دست می‌دهد:

\mathbf{E}(\mathbf{r}) = \frac{Q}{4\pi \varepsilon_0}\frac{\hat{\mathbf{r}}}{r^2}

که اساساً معادل قانون کولن می‌باشد.

ارسال شده در : پنج شنبه 24 مهر 1393 ساعت: 9:26 + تعداد بازديد : 218

نویسنده : حسین نوروزی

دسته بندی ها : ریاضی , ,

» نظرات()
می پسندم 0 نمی پسندم 0

انواع اعداد

اعداد حسابی

اعداد حسابی همان اعداد طبیعی هستند که صفر هم به آنها اضافه شده است. به عبارت دیگر به مجموعه‌ی اعداد زیر ،‌ اعداد صحیح یا اعداد درست گویند و آن را با Z نمایش می‌دهند:

{ ... , 3 , 2 , 1 , 0 , 1- , 2- , 3- , ...} = Z
درواقع اعداد صحیح شامل اعداد طبیعی مثبت و اعداد طبیعی منفی و عدد صفر است. این اعداد همانند اعداد طبیعی جزء مجموعه های شمارش پذیر نامتناهی است. شاخه ای از ریاضیات که به مطالعه در مورد ویژگی‌های اعداد صحیح می پردازدنظریه اعداد نام دارد.

صحیح همانند اعداد طبیعی نسبت به اعمال جمع و ضرب بسته است،یعنی جمع و ضرب هر دو عدد صحیح، یک عدد صحیح است. و چون اعداد صحیح شامل اعداد منفی و صفر می باشند بنابراین بر خلاف اعداد طبیعی نسبت به عمل تفریق نیز بسته اند.ولی چون حاصل تقسیم دو عدد صحیح بر هم ممکن است عددی صحیح نباشد،پس نمی‌تواند نسبت به عمل تقسیم بسته باشد.

اعداد طبیعی

اعداد طبیعی، اعدادی هستند که برای شمردن به کار می‌روند. مجموعه اعداد طبیعی {... ,۳ ,۲ ,۱} است.

در این مجموعه عدد صفر وجود ندارد و با اضافه کردن آن، مجموعه اعداد حسابی به وجود می‌آید. این مجموعه یک مجموعه نامتناهی است.

در ریاضیات، مجموعه اعداد طبیعی را با نماد N نمایش می‌دهند. این حرف از آغاز واژه انگلیسی Natural، به معنای طبیعی، گرفته شده است.

اعداد گنگ اعداد اصم

اعداد گنگ، یا اعداد اصم، اعدادی حقیقی هستند که گویا نباشند، یعنی نتوان آن‌ها را به صورت کسری که صورت و مخرجش عدد صحیح باشند نوشت. مجموعه اعداد گنگ مجموعه‌ای ناشمارا است ولي می‌توان اعداد گنگ را روي محور اعداد نمايش داد كار بسيار ساده ايي است كافي است هندسه را در رياضيات مورد استفاده قرار دهيم . امتحان كنيدميتوان از رابطه فيثاغورث استفاده كرد.
اعداد اول

اعداد اول اعدادی طبیعی هستند که بر هیچ عددی بجز خودشان و عدد ۱ بخش‌پذیر نباشند. تنها استثنا عدد ۱ است که جزو این اعداد قرار نمی‌گیرد. اگرعددی طبیعی وبزرگ‌تر از ۱ اول نباشد مرکب است.

عدد یکان اعداد اول بزرگ‌تر از ۱۰ فقط ممکن است اعداد ۱، ۳، ۷، ۹ باشد.

اعداد اول جزو یکی از معماهای ریاضی باقیمانده است و هنوز کسی به فرمولی برای آنها به دست نیاورده است.

سری اعداد اول به این صورت شروع می‌شود: ۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹ ...

قضیه ۱: تعداد اعداد اول بی‌نهایت است.

برهان: حکم را به روشی که منسوب به اقلیدس است اثبات می‌کنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد. حال عدد M را که برابر حاصل‌ضرب این اعداد به علاوه ۱ را در نظر بگیرید. این عدد مقسوم‌علیهی غیر از آن n عدد دارد که با فرض در تناقض است.

قضیه ۲ (قضیه اساسی حساب): هر عدد طبیعی بزرگ‌تر از ۱ را به شکل حاصل‌ضرب اعدادی اول نوشت.

قضیه ۳ (قضیه چپیشف):اگر n عددی طبیعی و بزرگ‌تر از ۳ باشد، حتما" بین n و ۲n عدد اولی وجود دارد. قضيه ۴ هر عدد زوج را می‌توان بصورت جمع سه عدد اول نوشت.

قضيه ۵ هر عدد فرد (شامل اعداد اول) را می‌توان به صورت جمع سه عدد اول نوشت (اثبات بر پايه قضيه ۴)

قضيه 6-هر عدد فرد را می‌توان به صورت دو برابر يك عدد اول بعلاوه يك عدد اول ديگر نوشت.

خواص اعداد اول

1- هر عدد اول برابر است با 6n+1 يا 6n-1 كه n يك عدد صحيح است.

2-مجذور هر عدد اول برابر است با 24n+1.

3-تفاضل مجذورهاي دو عدد اول مضربي از 24 است.

4-حاصلضرب هر دو عدد اول بجز 2و3 مضربي از 6 بعلاوه يا منهاي يك است.

توان چهارم هر عدد اول بجز 2و3 مضربي از 240 بعلاوه يك است.

بزرگ‌ترین عدد اول کشف شده برابر دو به توان ‪ ۳۰ميليون و ‪ ۴۰۲هزار و ‪ ۴۵۷منهاي يك است.این عدد یک عدد مرسن است. عدد مرسن عددی است که برابر 2 به توان n منهای یک است.

لازم به ذكر است كه تعداد 3000 عدد اول در سايت مگاسندرwww.megasender.org وجود دارد و افرادي كه مايل به دريافت بيشتر اين اعداد هستند مي توانند با سايت مذكور تماس گرفته و تعداد بيشتري از آنها را بر روي لوح فشرده دريافت نمايند و طراحان اين سايت خودشان اين اعداد را محاسبه نموده اند.
اعدد جبری

اعداد جبری در ریاضیات اعدادی هستند که جواب معادله‌ای به شکل زیر باشند:
anxn + an−1xn−1 + ··· + a1x + a0 = 0ضریب‌های a0 تا an در این معادله چند جمله‌ای اعداد گویا هستند.
تمام اعداد گویا اعداد جبری هم هستند. بعضی از اعداد حقیقی عدد جبری نیستند. عددی که جبری نباشد عدد متعالی (یا غیرجبری) نامیده می‌شود.

اعداد گویا

اعداد گویا1 حاصل تقسیم دو عدد صحیح بر یکدیگرست، به شرطی که عدد دوّم (مقسوم علیه) صفر نباشد. به بیان دیگر، هر عدد گویا را می‌توان به شکل a/b یا آ بيم نوشت (که a و b اعداد صحیح‌اند).

در ریاضیات، مجموعه اعداد گویا را، عموماً، با Q نمایش می‌دهند. به عنوان مجموعه‌ای شمارا (یا قابل شمارش)، ولی نامتناهی، مجموعهٔ اعداد گویا، خود، زیرمجموعه‌ای‌ست چگال (dense) از مجموعهٔ بزرگ‌تر و عمومی‌تر اعداد حقیقی.

اعداد صحیح

مجموعهٔ اعداد صحیح به اجتماع مجموعهٔ اعداد طبیعی، قرینهٔ اعداد طبیعی ، و {0} (مجموعه ای که تنها عدد صفر عضو آن است) گفته می*شود. در ریاضیّات، معمولاً این مجموعه را با Z یا (ابتدای کلمه آلمانی Zahlen به معنی اعداد) نشان می*دهند. همانند مجموعهٔ اعداد طبیعی، مجموعهٔ اعداد صحیح نیز یک مجموعهٔ شمارای نامتناهی*ست.
شاخه*ای از ریاضیّات که به مطالعهٔ اعداد صحیح می*پردازد، نظریهٔ اعداد نام دارد.
خواص جبری
همانند اعداد طبیعی، نیز نسبت به دو عمل جمع و ضرب بسته است. این بدان معناست که حاصل جمع و حاصل ضرب دو عدد صحیح، خود، یک عدد صحیح است. بر خلاف مجموعهٔ اعداد طبیعی، از آنجا که اعداد صحيح منفی، و به ویژه، عدد صفر هم به تعلق دارند، این مجموعه، نسبت به عمل تفریق نیز بسته است. اما تحت عمل تقسیم بسته نیست، زیرا خارج قسمت تقسیم دو عدد صحیح، لزوما عددی صحیح نخواهد بود.
برخی از خواصّ اساسی مربوط به عملیّات جمع و ضرب در جدول زیر گنجانیده شده است (در اینجا b ،a، و c اعداد صحیح دل*خواه هستند:)
جمع ضرب
بسته بودن:
a + b یک عدد صحیح است a × b یک عدد صحیح است
شرکت پذیری:
a + (b + c) = (a + b) + c a × (b × c) = (a × b) × c
تعویض پذیری:
a + b = b + a a × b = b × a
وجود یک عنصر واحد:
a + 0 = a a × 1 = a
وجود یک عنصر عکس:
a + (−a) = 0
توزیع پذیری:
a × (b + c) = (a × b) + (a × c)
نداشتن مقسوم علیه*های صفر:
اگر ab = 0، آنگاه a = 0 یا b = 0
مطابق جدول بالا، خواصّ بسته بودن، شرکت پذیری و جابه جایی (یا تعویض پذیری) نسبت به هر دو عمل ضرب و جمع، وجود عضو همانی (واحد، یا یکّه) نسبت به جمع و ضرب، وجود عضو مع*** فقط نسبت به عمل جمع، و خاصیّت توزیع پذیری ضرب نسبت به جمع از اهمیت برخوردارند.

اعداد مرکب

عدد مرکب عددی طبیعی بجز یک است که اول نباشد.

پانزده عدد مرکب اول عبارت‌اند از:

۴, ۶, ۸, ۹, ۱۰, ۱۲, ۱۴, ۱۵, ۱۶, ۱۸, ۲۰, ۲۱, ۲۲, ۲۴ و ۲۵

قانون برای تمام اعداد مرکب وبزرگ ‌تر از ۵(فقط ۴ از این قاعده پیروی نمی‌کند) صدق می‌کند.

اعداد حقیقی

مجموعه اعداد حقیقی که با R نمایش داده می شود و شامل کلیه ی اعداد صحیح,گویا,طبیعی و حسابی و همچنین شامل R-Q است که اعدادگنگ یا اصم می باشد می شود

ارسال شده در : سه شنبه 22 مهر 1393 ساعت: 15:35 + تعداد بازديد : 322

نویسنده : حسین نوروزی

دسته بندی ها : ریاضی , ,

» نظرات()
می پسندم 0 نمی پسندم 0

دنباله فیبوناتچی

در دوران حیات فیبوناچی مسابقات ریاضی در اروپا بسیار مرسوم بود در یکی از همین مسابقات که در سال ۱۲۲۵ در شهر پیزا توسط امپراتورفردریک دوم بر‌گزار شده بود مسئله زیر مطرح شد:

«فرض کنیم خرگوش‌هایی وجود دارند که هر جفت (یک نر و یک ماده) از آنها که به سن ۱ ماهگی رسیده باشند به ازاء هر ماه که از زندگی‌شان سپری شود یک جفت خرگوش متولد می‌کنند که آنها هم از همین قاعده پیروی می‌کنند حال اگر فرض کنیم این خرگوشها هرگز نمی‌میرند و در آغاز یک جفت از این نوع خرگوش در اختیار داشته باشیم که به تازگی متولد شده‌اند حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت.»

فرض کنیم xn تعداد جفت خرگوش پس از n ماه باشد، میدانیم که x_۲=۱,x_۱=۱، تعداد جفت خرگوشها در ماه n+۱ ام برابر خواهد بود با حاصل جمع تعداد جفت خرگوشهایی که در این ماه متولد می‌شوند با تعداد جفت خرگوشهای موجود(x_n).اما چون هر جفت خرگوش که از دو ماه قبل موجود بوده هم اکنون حداقل دوماه سن خواهند داشت و به سن زادو ولد رسیده‌اند تعداد جفت خرگوش های متولد شده برابر خواهد بود با xn-۱، پس خواهیم داشت:

x_۱ = ۱ , x_۲ = ۱ , x_n + ۱ = x_n + x_n - ۱

که اگر از قواعد مذکور پیروی کنیم به دنباله زیر خواهیم رسید که به دنباله فیبوناچی مشهور است.

۱, ۱, ۲, ۳, ۵, ۸, ۱۳, ۲۱, ۳۴, ۵۵, ۸۹, ۱۴۴, ۲۳۳, ۳۷۷, ۶۱۰, ۹۸۷, ۱۵۹۷, ۲۵۸۴,…

فیبوناچی با حل این مسئله از راه حل فوق دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفت‌انگیز و کاربردهای فراوان آن تا به امروز نه تنها نظر ریاضی‌دانان بلکه دانشمندان بسیاری از رشته‌های دیگر را به خود جلب کرده.

رابطهٔ دنبالهٔ فیبوناچی به این شکل است:

F_1=F_2=1,\forall n>2: F_n=F_{n-1}+F_{n-2}

برای مثال برای به دست آوردن جملهٔ دهم باید جملهٔ نهم (۳۴) و جملهٔ هشتم (۲۱) را با هم جمع کنیم که برابر ۵۵ می‌شود.

جمله عمومی دنباله فیبوناچی[ویرایش]

چند فرمول برای احتساب جملهٔ nام دنبالهٔ فیبوناچی، بدون استفاده از جملات ماقبل وجود دارد.

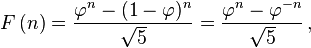F\left(n\right) = {{\varphi^n-(1-\varphi)^n} \over {\sqrt 5}}={{\varphi^n-\varphi^{-n}} \over {\sqrt 5}}\, ,

، یکی از این فرمول هاست.

\varphi

(فی) همان عدد طلایی است که برابر با :

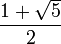{{1+\sqrt 5}}\over 2

می‌باشد.

ارتباط عدد طلایی با دنباله فیبوناچی[ویرایش]

روشهای متفاوتی برای بیان رابطه بین عدد طلایی و دنباله فیبوناچی وجود دارد که ما در اینجا به دو نمونه بسنده می‌کنیم.

نسبت دو عضو متوالی دنباله[ویرایش]

اولین مطلبی که در زمینه ارتباط با دنباله فیبوناچی قابل ذکر است به این قرار است: دنباله را بار دیگر در نظر می‌بینیم:

۱۰----۹----۸----۷----۶----۵----۴----۳----۲----۱----شماره جمله

۵۵----۳۴----۲۱----۱۳----۸----۵----۳----۲----۱----۱----مقدار جمله

نسبت جمله دوم به اول برابر است با ۱

نسبت جمله سوم به دوم برابر است با ۲

نسبت جمله چهارم به سوم برابر است با ۱٫۵

نسبت جمله پنجم به چهارم برابر است با ۱٫۶۶

نسبت جمله ششم به پنجم برابر است با ۱٫۶

نسبت جمله هفتم به ششم برابر است با ۱٫۶۲۵

نسبت جمله هشتم به هفتم برابر است با ۱٫۶۱۵

نسبت جمله نهم به هشتم برابر است با ۱٫۶۱۹

نسبت جمله دهم به نهم برابر است با ۱٫۶۱۷

به نظر می‌رسد که این رشته به عدد طلایی نزدیک می‌شود. اگر نسبت عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد ۱٫۶۱۸۰۳۳۹۸۸۷۴۹۸۹۵ می‌رسیم که با تقریب ۱۴ رقم اعشار نسبت طلایی را نشان می‌دهد. نسبت جملات متوالی به عدد طلایی میل می‌کند.

معادله خط[ویرایش]

معادلهٔ خطی به صورت y=mx در نظر می‌گیریم. m به معنی شیب خط است و یک عدد حقیقی است. می‌دانیم اگر m گنگ باشد، خط y=mx از هیچ نقطه‌ای با مختصات صحیح به جز مبدأ عبور نخواهد کرد. در واقع این خط امکان ندارد از نقطه‌ای (جز مبدأ) عبور کند که هم x و هم y آن عدد صحیح باشند.
حال به جای m قرار می‌دهیم: φ. یعنی خط y=φx را در نظر می‌گیریم. چون φ هم یک عدد گنگ است، این خط از هیچ نقطه‌ای با x و y صحیح (جز مبدأ) عبور نخواهد کرد. به همین دلیل نقطه‌هایی را با x و y صحیح در نظر می‌گیریم که کمترین فاصله را از این خط دارند. ابتدا به نظر می‌رسد نقطهٔ (۱، ۱) کمترین فاصله را با این خط دارد. ولی فاصلهٔ نقطهٔ (۲، ۱) از این خط کمتر است. نقطهٔ (۳، ۲) فاصلهٔ کمتری با این خط دارد. همچنین فاصلهٔ نقطهٔ (۵، ۳) از این هم کمتر است. این نقاط به همین ترتیب ادامه خواهند یافت و در زیر چند نقطهٔ بعدی را که فاصله‌شان از این خط کمتر می‌شود را می‌بینید:...،(۵۵، ۳۴)، (۳۴، ۲۱)، (۲۱، ۱۳)، (۱۳، ۸)، (۸، ۵)، (۵، ۳)، (۳، ۲)، (۲، ۱)، (۱، ۱)

صحت مطالب فوق به راحتی قابل بررسی است. با کمی دقت در مختصات این نقاط درخواهیم یافت که این مختصات از الگوی دنباله فیبوناچی پیروی می‌کنند. این نقاط را نقاط فیبوناچی می‌نامند.

ارسال شده در : سه شنبه 22 مهر 1393 ساعت: 15:14 + تعداد بازديد : 101

نویسنده : حسین نوروزی

دسته بندی ها : ریاضی , ,

» نظرات()
می پسندم 0 نمی پسندم 0

عدد طلایی

یکی از کلیشه‌ای‌ترین و شاید تاریخی‌ترین سوال‌های دانش‌آموزان درخصوص درس ریاضی این است که ریاضی و فرمول‌های متعدد آن در زندگی ما چه کاربردی دارد.

برای پاسخگویی به این سوال با همکاری دانش آموزان دبیرستان نمونه دولتی حیدری موسوی شهرستان هشترود، کارگاهی آموزشی درباره عدد 1.618 و کاربردهای آن برگزار کردیم. گذشته از نحوه گروه بندی، اجرا و جزئیات این طرح ـ که برای نخستین بار در آموزش و پرورش کشور انجام شد ـ در این طرح که طرحی نو در آموزش ریاضی است، موضوعات مختلف و کاربردی- ریاضی درسیکه در سطح بین الملل نیز دارای تازگی و پویایی است ـ مورد بررسی قرار گرفت.

نسبت طلایی یا همان عدد 1.618 یکی از زیبایی های دنیای ریاضی است که در گوشه و کنار این دنیای بزرگ از اندام های بدن انسان تا آثار برجسته و مشهور هنری و معماری در سطح دنیا و حتی نحوه رشد دانه های گل آفتابگردان می توان ردپایی از آن پیدا کرد. بسیاری از کارشناسان بر این باورند هر اثر هنری که در آن نسبت طلایی رعایت شده باشد، منحصر به فرد است. جالباین که در کاغذهای استاندارد سری A نیز نسبت طول به عرض با نسبت طلایی برابر است. به همین دلیل، محققان بر این باورند زیباترین سطوح و اشکال آنهایی است که نسبت طلایی در آنها به کار رفته باشد.

عدد 1.618 که به عدد یا نسبت طلایی یا نسبت فیبوناچی نیز شهرت دارد، حاصل تلاش دانشمندانی ازجمله اقلیدس، لوکاپاچیولی و لئوناردو فیبوناچی است. شما می توانید در حوزه های مختلف ردپایی از نسبت طلایی را پیدا کنید. یکی از این حوزه ها هندسه است. اگر در پاره خطی، نسبت قسمت بزرگ تر به کوچک تر برابر با نسبت کل خط به قسمت بزرگ باشد، این نسبت قطعا عدد طلایی است.

یکی دیگر از حوزه هایی که نشانی از نسبت طلایی در آن پیدا می کنید، دنباله فیبوناچی است. در این دنباله که عبارت است از 1، 1، 2، 3، 5، 8، 13، 21 و... اگر اعداد پس از 2 را در نظر بگیریم و هر کدام را به عدد ماقبل خود تقسیم کنیم، شاهد اعدادی بسیار نزدیک به عدد نسبت طلایی یا 1.618 خواهیم بود. هر چه بیشتر این تقسیم را ادامه دهید، عدد حاصل به نسبت طلایی نزدیک تر می شود.

گذشته از این در بسیاری از ساختارهای هستی می توانید نشانی از نسبت طلایی پیدا کنید؛ از مارپیچ های دی ان ای گرفته تا مارپیچ گوش انسان، حلزون، ساختار مارپیچی کهکشان ها و تمام زیبایی های طبیعت ازجمله برگ های درختان، خطوط و نقش و نگار روی پرهای طاووس و مارپیچ های آفتابگردان این نسبت رعایت شده است. این عدد در معماری باستان و معاصر ایران و جهان نیز کاربرد فراوانی داشته است. از آن جمله می توان به هرم جیزا در مصر، برج آزادی تهران، قلعه دالاهو در کرمانشاه، بنای بیستون کرمانشاه و مقبره ابن سینا در همدان اشاره کرد. برای مثال ابعاد بنای بیستون کرمانشاه پنج کیلومتر در سه کیلومتر ذکر شده که اعداد چهارم و پنجم دنباله فیبوناچی اند. با تقسیم این دو عدد به عدد 1.6 می رسیم که بسیار نزدیک به عدد طلایی است.

این عدد در بدن انسان نیز بسیار کاربرد دارد. زیبایی چهره، زیبایی خنده، تناسب اندام و خوش تیپی همه و همه از شاهکارهای الهی در آفرینش انسان است. اگر نگاهی به تاریخچه عدد طلایی بیندازید، می بینید لئوناردو داوینچی اولین نفری است که نسبت دقیق استخوان های انسان را اندازه گیری و ثابت کرد این نسبت ضریبی از عدد طلایی است. در سنجش تناسب اندام خود می توانید فاصله انگشتان پا تا ناف را بر فاصله ناف تا بالای سر تقسیم و حاصل را با عدد 1.618 مقایسه کنید. هر چه این عدد به 1.618 نزدیک تر باشد به این معنی است که شما تناسب اندام خوبی دارید. چنین نشانه هایی که در آنها می توان به نسبت طلایی رسید، در بدن انسان بسیار زیاد است. یکی از دیگر ویژگی های جالب توجه نسبت طلایی این است که اگر فاصله شهر مکه تا قطب شمال را بر فاصله این شهر تا قطب جنوب تقسیم کنیم، عددی بسیار نزدیک به عدد طلایی به دست می آید. بر این اساس می توان گفت شهر مکه در نقطه طلایی زمین قرار دارد. علاوه بر این، بررسی های انجام شده نشان داده است شهر مکه در نقطه طلایی عربستان و بنای کعبه در نقطه طلایی شهر مکه قرار دارد.

ارسال شده در : سه شنبه 22 مهر 1393 ساعت: 15:0 + تعداد بازديد : 99

نویسنده : حسین نوروزی

دسته بندی ها : ریاضی , ,

» نظرات()
می پسندم 0 نمی پسندم 0

لیست صفحات

تعداد صفحات : 1

صفحه قبل 1 صفحه بعد

لحظات خوشی را در سایت برایتان آرزو میکنیم

ورود کاربران

نام کاربری

رمز عبور

رمز عبور را فراموش کردم ؟

عضويت سريع

آرشیو

نویسندگان
- حسین نوروزی

آمار

آمار مطالب

کل مطالب : 13

کل نظرات : 0

آمار کاربران

افراد آنلاین : 1

تعداد اعضا : 0

آمار بازدید

بازدید امروز : 10

بازدید دیروز : 0

ورودی امروز گوگل : 1

ورودی گوگل دیروز : 0

بازدید هفته : 10

بازدید ماه : 28

بازدید سال : 95

بازدید کلی : 19157

اطلاعات شما

آی پی : 3.147.47.82

مرورگر :

سیستم عامل :

امروز :

جدید ترین مطالب

مطالب پربازدید

مطالب تصادفی

صفحات جانبی

ریاضی

خبرنامه

براي اطلاع از آپيدت شدن سایت در خبرنامه سایت عضو شويد تا جديدترين مطالب به ايميل شما ارسال شود
تبادل لینک هوشمند

کتاب علوم هشتم وآزمایش های مربوط به آن

عدد اول

محتویات

قضیه‌ها[ویرایش]

قضایای اعداد اول[ویرایش]

تابع شمارش اعداد اول[ویرایش]

قضیه اعداد اول (prime number theorem)[ویرایش]

قضیه ویلسون راهی برای تشخیص اعداد اول[ویرایش]

کشف و محاسبه[ویرایش]

جایزه‌ها برای پیدا کردن اعداد اول[ویرایش]

الگوهای توزیع اعداد اول[ویرایش]

قانون گاوس

محتویات

از دیدگاه بار کل[ویرایش]

فرم انتگرالی[ویرایش]

به کارگیری فرم انتگرالی[ویرایش]

فرم دیفرانسیلی[ویرایش]

هم ارزی فرم دیفرانسیلی و انتگرالی[ویرایش]

از دیدگاه بار آزاد[ویرایش]

بار آزاد در مقابل بار مقید[ویرایش]

فرم انتگرالی[ویرایش]

فرم دیفرانسیلی[ویرایش]

بیان هم ارزی بار کل و بار آزاد [ویرایش]

در مواد خطی[ویرایش]

ارتباط با قانون کولن[ویرایش]

استخراج قانون گاوس از قانون کولن[ویرایش]

استخراج قانون کولن از قانون گاوس[ویرایش]

جمله عمومی دنباله فیبوناچی[ویرایش]

ارتباط عدد طلایی با دنباله فیبوناچی[ویرایش]

نسبت دو عضو متوالی دنباله[ویرایش]

معادله خط[ویرایش]

موضوعات

ورود کاربران

عضويت سريع

آرشیو

نویسندگان

آمار

پشتيباني آنلاين

جستجو

جدید ترین مطالب

مطالب پربازدید

مطالب تصادفی

صفحات جانبی

امکانات جانبی

درباره ما

خبرنامه

تبادل لینک هوشمند

لینک دوستان

پیوندهای روزانه

آخرین نظرات کاربران